Slow Papers: Exploration by Random Network Disillation

1 개요

강화학습의 매력은 별다른 데이터 없이 에이전트를 환경에 놓고 충분한 학습을 거치면 reward를 최대화하는 방법을 찾는다는 것입니다. 하지만 그렇기 때문에 환경의 reward가 제대로 설계되지 않았다면, 강화학습 에이전트는 학습을 하는 것이 어렵습니다. 현재 널리 쓰이는 몬테주마의 복수 (Montezuma’s Revenge) 가 그러한 환경이 가장 큰 예시죠. 아래 화살표대로 열쇠를 잡을 때까지, 아무런 보상이 주어지지 않기 때문에, 에이전트는 “우연히” 저 열쇠를 얻기 전까지 어느 행동이 올바른 건지 알 수 없습니다.

이러한 문제점을 보완하기 위해서, 지난 몇 년간 많은 저명한 강화학습 연구자들은 무작위한 탐험이 아니라, 방향이 유도된 탐험 (guided exploration) 방식을 고안해내었습니다. 그 중에는 이미 환경을 잘 알고 있는 고수의 발걸음을 따라가는 Imitation Learning 이나, 에이전트에게 하나의 스케쥴을 제공해주는 Curriculum Learning 등이 있습니다.

이번에 소개할 Exploration by Random Network Distillation 의 논문은, 호기심 (curiosity) 을 수치화시켜서, 에이전트가 여태껏 경험하지 못한 것을 우선시하게끔 하는 방법입니다. 기존 알고리즘들에서 탐험은 보상을 최대화하기 위해 하는 최소한의 탐험입니다. 호기심을 가진 에이전트를 만든다는 것은, 이 보상에 탐험 보너스 (exploration bonus) 를 준다는 것입니다. 에이전트가 새로운, 흥미로운 state라면, 호기심을 충족시켰다는 의미로 내부적인 보상을 주는 것입니다.

next_state, ext_reward, done, info = env.step(action) # 환경과의 상호작용으로 얻는 외부 보상
int_reward = self._compute_int_reward(next_state) # 호기심에 의한 내부 보상
reward = ext_reward + int_reward # 최대화할 보상 = 외부 보상 + 내부 보상

호기심을 수치화시킨 논문은 예전에도 많이 있었는데, 이 논문의 차별점은 다음과 같습니다.

무작위로 초기화된 인공신경망 (random network)을 통한 호기심 수치화 방법
몬테주마의 복수 에서 state-of-the-art 성능

2 Random Network Distillation

2-1 직관적인 이해

Random Network Distillation 을 한국말로 의역하면, 무작위 인공신경망의 정보를 추출하는 것입니다. 여기서 무작위 인공신경망이란, 무작위로 초기화되었다는 것을 의미합니다. 즉, 아무런 학습이 되지 않은 상태입니다. 직관적인 이해를 돕기 위해, 입력이 숫자 1개, 출력이 숫자 1개인 간단한 인공신경망을 만들어봅시다.

rnd_target_net = RNDNetwork() # 초기화된 상태

이 인공신경망의 출력을 예측해보는 일을 맡았다고 (predictor) 가정해 봅시다. 이 인공신경망에 1이라는 입력을 준다면, 어떤 출력이 나올까요? 글쎄요, 무작위로 초기화되었기 때문에, 예측하기란 불가능합니다. 그렇다면 우리가 알 방법은 인공신경망의 출력을 확인하는 것밖에 없습니다.

> rnd_target_net([[1]])
[[3]]

3이라는 출력이 나오네요! 그러면 다시 똑같은 질문을 드리겠습니다. 이 똑같은 인공신경망에 1이라는 입력을 준다면, 어떤 출력이 나올까요? 이제는 우리가 3이라는 출력이 다시 나올 것이라는 것을 확신할 수 있습니다. 같은 입력에 다른 출력이 나올리는 없으니까요.

이번에는 약간 다른 질문을 드리겠습니다. 입력을 1 대신 1.00000001을 준다면 어떤 출력이 나올까요? 정확하게 예측할 수는 없지만, 아마 3에 근접한 숫자가 나올 것입니다. 그렇다면 1.0001을 입력으로 준다면? 더 불확실하지만, 3에 근접한 숫자가 나오지 않을까요? 입력을 10을 준다면? 글쎄요. $(1, 3)$ 이라는 입출력으로만 예측하기는 너무 어려울 것 같네요.

예측하기 어렵다는 말을 오류의 개념으로 바꿔 설명할 수도 있습니다. 예측의 오류를 이렇게 Mean Squared Error (MSE) 처럼 정의할 수 있습니다.

$\text{Error}(\text{input}) = \left(\text{target}(\text{input}) - \text{predictor}(\text{input})\right)^2$

이미 $\text{target}(1)$ 의 값을 알고 있기 때문에, $\text{Error}(1) = 0$ 입니다. 그리고 아마 $\text{Error}(1.00000001) < \text{Error}(1.0001) « \text{Error}(10)$ 일 것입니다. 즉, 알고 있는 입력에서 멀리 벗어날수록, 오류값이 커집니다.

2-2 호기심

위의 오류를 어떻게 호기심과 연관지을 수 있을까요? 이제는 입력이 단순한 숫자가 아니라 환경과 상호작용하면서 보는 state입니다. 출력은 하나의 k-dimensional vector 입니다. 위에서 내린 결론에 따르면, 알고 있는 state와 많이 다를수록, 오류값이 커집니다. 이것을 바꿔 말한다면, 오류값이 큰 state는, predictor가 아직 유사한 것을 많이 보지 못한 state입니다. 즉, 오류값이 높은 state가 호기심을 충족시키는 state입니다.

그렇다면, 호기심에 의한 내부 보상을 어떻게 정의하면 좋을까요? 이 논문은 오류값을 그대로 내부 보상으로 정의하는 것을 제안합니다.

target = rnd_target_net(next_state)
prediction = ???

int_reward = F.mse_loss(target, prediction)

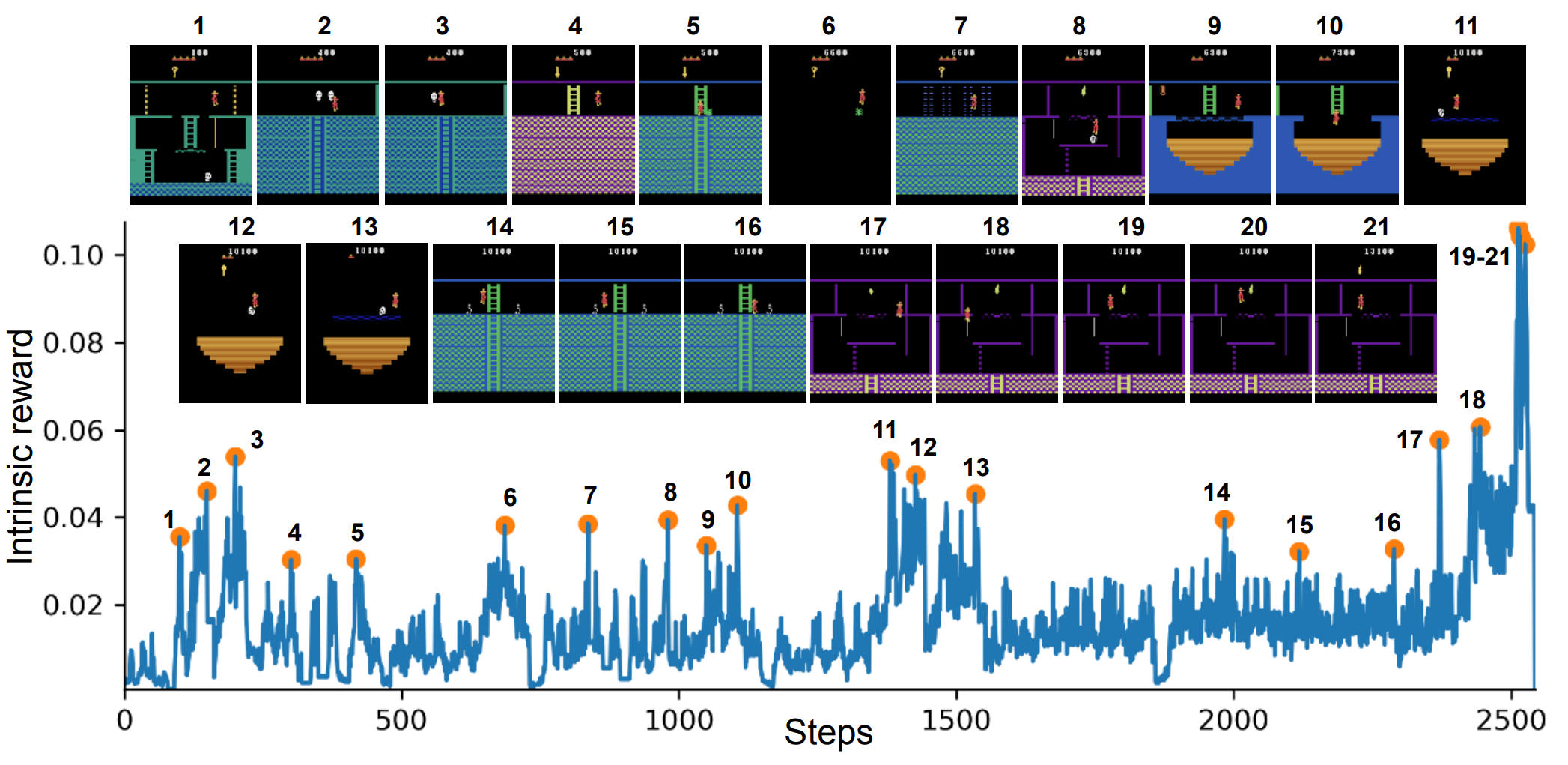
몬테주마의 복수의 환경에서 내부 보상을 살펴보면, 유의미한 이벤트가 발생할 때 내부 보상이 높은 것을 볼 수 있습니다. (2, 8, 10, 21) 은 life를 잃을 때, (3, 5, 6, 11, 12, 13, 14, 15) 는 적을 아슬아슬하게 피할 때, (7, 9, 18) 은 어려운 장애물을 피할때, 그리고 (19, 20, 21) 은 아이템을 습득할 때 입니다.

2-3 Predictor

지금까지 이 과정에서 predictor는 우리였습니다. 이미 알고있는 입출력 값을 통해서, 다른 입력값에 대한 출력값을 예측했죠. 당연히, 실제 강화학습에서 사람이 이렇게 매번 예측을 하는 것은 비실용적입니다. 그러면, 우리와 비슷한 predictor를 어떻게 표현할 수 있을까요?

Predictor의 역할을 다시 한 번 살펴봅시다. Predictor는 주어진 입출력에 대하여 target function을 근사하는, 하나의 function approximator 입니다. 또, 이 function approximator는 주어진 입출력으로 supervised learning 을 합니다. 이렇게 보면, predictor 역시 하나의 인공신경망으로 표현하는게 자연스럽다는 걸 알 수 있습니다.

def _compute_int_reward(self, next_state):
    """
    주어진 `next_state`로 RND의 내부적인 보상을 계산해 반환한다.
    
    Parameters
    ----------
    next_state: torch.FloatTensor
    	환경으로부터 받은 state.

    Returns
    -------
    int_reward : torch.FloatTensor
    	RND로 계산한 내부 보상.
    """
    target = rnd_target_net(next_state)
    prediction = rnd_predictor_net(next_state)
    
    return F.mse_loss(target, prediction)

Predictor network의 크기가 target network보다 작으면 어떻게 될까요? 그렇다면, 인공신경망 크기의 한계로 인해, 아무리 많은 데이터가 있어도, target network의 출력값을 예측하지 못합니다. 크기차이로 인하여 오류가 발생하는 것입니다. 우리는 이 오류를 호기심에 의한 내부 보상으로 사용하기 때문에, 크기차이로 인한 오류는 noise로, 학습을 방해할 수 있습니다.

Predictor network의 크기가 target network보다 크다면, 이러한 걱정은 할 필요가 없겠죠. 하지만, 과다하게 크게 만든다면, 내부 보상을 계산하는데 시간을 너무 많이 쓰게 됩니다. 그렇기 때문에, predictor network와 target network 모두 동일한 architecture를 사용합니다.

rnd_target_net = RNDNetwork()
rnd_predictor_net = RNDNetwork()

3 세부 설계

3-1 PPO

지금까지 얘기한 RND는 어떻게 보면 에이전트와는 무관합니다. 단순히 환경이 주는 보상을 바꾸는 것이기 때문이죠. 즉, 이 보상을 가지고 어떻게 학습할지는 에이전트에 달렸습니다. 이 논문의 저자는 수많은 알고리즘들 중 Proximal Policy Optimization (PPO) 를 사용하였습니다. PPO는 policy gradient 알고리즘 중 하나로, 간략하게나마 설명하자면 두 가지 특징이 있습니다.

Policy 가 한 업데이트에 너무 급격하게 변하는 것을 막고자 objective function 을 “clip” 합니다.
$T$개의 timestep 동안의 경험을 모아서, $K$ 번의 epoch 으로 업데이트합니다.

From *Proximal Policy Optimization Algorithms* (Schulman et al., 2017)

RND와 PPO를 합치는 것으로, 이 논문의 에이전트가 완성이 됩니다.

3-2 Discount Factor

RND가 테스트되는 환경들은 아타리 2600의 게임들 중 외부 보상을 얻기 굉장히 어려운 환경들입니다. 그렇기 때문에, discount factor가 기존의 $0.99$의 값을 가질 경우, 몇 백 스텝 뒤에 있는 보상을 계산하기 어렵습니다. 그래서, 저자들은 외부 보상에 한해서 discount factor를 $0.999$ 로 증가시키는 것을 제안합니다.

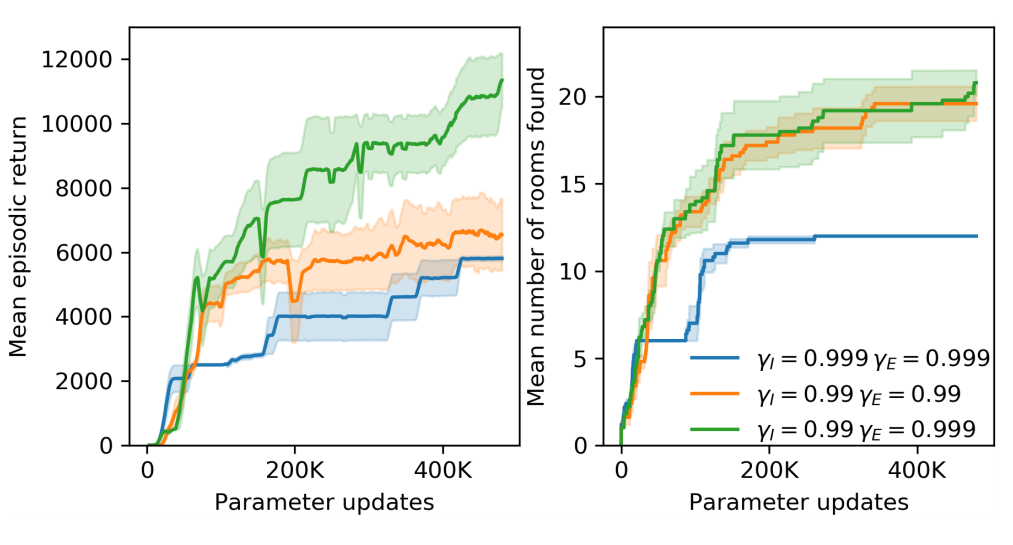
하나의 hyperparameter만 수정했을 뿐인데, 얻는 총 보상이 두배 정도로 증가하는 것을 볼 수 있습니다.

3-3 결과

PPO에 RND를 추가하면 어느 정도 결과가 나올까요? 강화학습의 특성상, random seed에 따라 천차만별의 결과가 나오기 때문에, 하나의 최고기록으로 판별하기는 어렵습니다. 하지만, RND는 24개의 방을 모두 탐험하면서 17500이라는 점수를 얻고 첫 레벨을 통과한 첫번째 에이전트이기 때문에, 충분히 주목할 만한 결과라고 생각합니다.

4 실패한 아이디어들

이 논문에 적힌 테크닉들 전부가 생각했던 대로 성능을 향상시키지는 않았다고 합니다. 이 섹션에서는 예상 외로 효과가 미미한 테크닉들을 서술합니다.

4-1 Recurrence

몬테주마의 복수라는 게임은 기본적으로 partially observable한 게임입니다. 이 게임은 다양한 방이 있고, 그 방에서 소품을 얻고, 문을 열어야 하는 게임입니다. 이 게임에서 observation은 화면으로 제공되는데, 화면에는 현재 속한 방밖에 보이지 않습니다. 즉, 다른 방에 있는 소품의 유무나, 문이 열림/닫힘은 알 수 없죠. 그렇기 때문에, 저자들은 RNN을 써서 이 문제를 해소하면, 성능이 더 높아지지 않을까 생각했습니다.

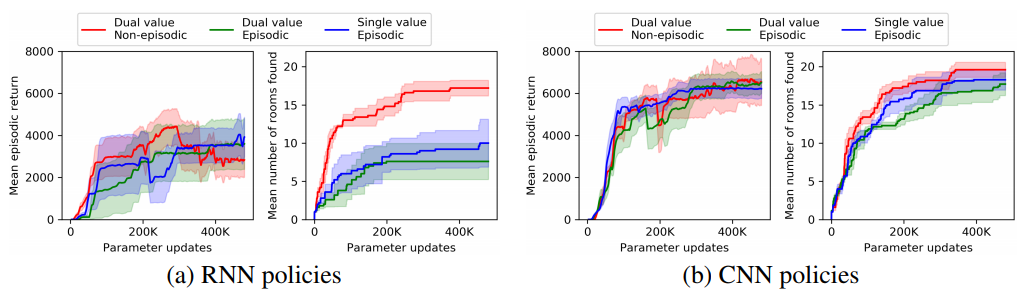
놀랍게도, RNN을 추가했을 때 기존 성능의 반밖에 학습하지 못하는 결과가 나옵니다.

4-2 외부 보상 vs. 내부 보상

외부 보상과 내부 보상은 내포하는 의미가 굉장히 다릅니다. 외부 보상은 환경이 주는 보상이고, 내부 보상은 호기심에 의한 보상입니다. 근원이 완전이 다른 두 보상들의 합을 하나의 $V(s;\theta)$ 로 근사하는 건 너무 어려운 일이 아닐까요? 그래서, 저자들은 외부 보상과 내부 보상을 나누는 방법을 제안합니다.외부 보상들의 합과 내부 보상들의 합을 따로 근사해서, 그 둘의 합으로 총 보상의 합을 근사하는 것이죠. 그래서 $V$를 계산할 때, 마지막에 두개의 숫자를 출력하고, 그 둘의 합을 사용합니다.

$V_{\text{total}}(s; \theta, \theta_I, \theta_E) = V_{I}(s;\theta, \theta_I) + V_{E}(s; \theta, \theta_E)$

이렇게 되면 내부 보상과 외부 보상을 구분짓는 것이 가능해집니다. 이에 그치지 않고, 저자들은 하나의 수정안을 더 제시합니다. 내부 보상을 episodic 하게 생각하지 말고, non-episodic하게 문제를 바꾸자는 것입니다.

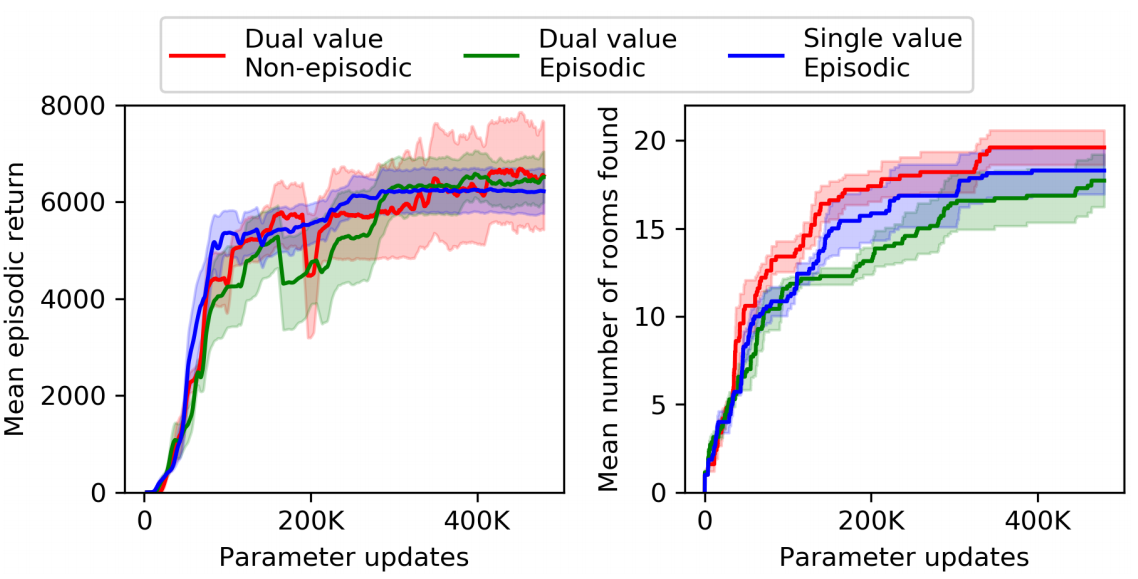
결과적으로, 단순히 합치는 것보다 두 보상의 기댓값들을 따로 계산하는 것이 더 좋지는 않습니다.

5 결론

RND는 굉장히 간단한 방법으로 내부 보상을 수치화시켜서 탐험을 효율적으로 하게 만들면서, 몬테주마의 복수에서 기존 SOTA를 아득히 뛰어넘는 훌룡한 성능을 보여주었습니다. 하지만 RND 역시 보완할 점이 많은 알고리즘입니다. 기존 SOTA를 뛰어넘었다고 하지만, 기존 SOTA들보다 훨씬 많은 양의 학습을 거쳤기 때문에, sample efficiency의 측면에서는 큰 발전이 없었습니다. 또, 몬테주마의 복수라는 한 환경에 중점을 두고 실험했기 때문에, 다른 환경에서 이정도의 효과를 기대하기 어렵습니다.

더 본질적인 문제로는 RND는 찾기 어려운 state를 찾았을 때 보상을 주기만 할 뿐, 이 state를 어떻게 찾을 지 방법을 제시하지는 않습니다. 그러므로, 단기적인 탐험에 대한 좋은 방법을 제시하기는 하지만, 장기적인 탐험에 대한 해결책이 되지 않습니다. 이러한 탐험 문제를 해결한다면, 강화학습이 실세계에서 적용되는 데 큰 역할을 할 것이라고 생각합니다.

RND를 직접 돌려보고 싶다면, 코드를 seungjaeryanlee/random-network-distillation-pytorch에 공개되어 있습니다! OpenAI의 TensorFlow 코드는 openai/random-network-distillation에 있습니다.